Bars and Spaces
All bar codes are comprised of bars and spaces (dark and light regions). A bar is a continuous dark area, a space is a continuous light area. From here on, I will refer to bar and/or space as simply bar. Most bar codes have a fixed number of possible bar widths. That is, each and every bar must be one of a fixed number of sizes. Each bar's width must also be a multiple of the smallest bar width. For instance, if the narrowest bar is 10 mil, then possible bar widths can be 10 mil, 20 mil, 30 mil, 40 mil, etc... But not, 15mil, or 25mil since these sizes are not multiples of the narrowest bar size of 10 mil.
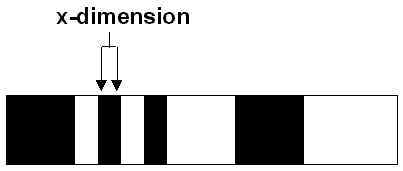
X Dimension
The width of the smallest bar is defined as a bar code's 'X' dimension. Each X' dimension is sometimes referred to as a module. In the following picture, you can easily pick out the smallest, or narrowest bar. By measuring this bar, we can determine the bar codes 'X' dimension. You can also see that all of the other bar widths are multiples of the smallest bar or 'X' dimension. Each bar's width is often expressed relative to the 'X' dimension, for instance, 3X refers to a bar that is 3times as wide as the narrowest bar.
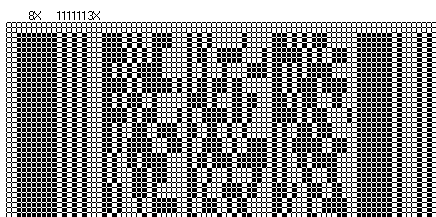
The following picture is a PDF417 bar code that looks like it is printed on graph paper. This image makes it easier to count the number of 'X' dimensions, or modules in each bar. If we look closely, we will see that each and every bar is an exact multiple of the minimum bar width. The first bar is 8X wide, the following space 1X wide, etc... In a validly printed code, without inkspread, you should never see a bar that is 1.5X, 4.2X, or not a whole multiple of X. In a PDF417 symbol , you will always see 1X, 2X, 3X, 4X, 5X, 6X, 7X, or 8X bars. Keep this in mind, you will see later how to detect, and avoid printing problems related to this topic. (See Scaling Errors)